Identificação de motores

O controle de motores não é uma ciência nova. No entanto, pode ser difícil entender o básico quando os cursos de graduação ensinam apenas a realizar o controle de fórmulas genéricas, cheias de números que não significam nada.

Fiz este artigo com base numa pesquisa que fiz com um amigo. Depois de muitas matérias e aulas de controle, não sabíamos como controlar um simples motor, que faz parte de 99% dos sistemas de controle práticos.

Enfim, chegamos a uma conclusão: precisávamos transformar o motor em uma equação controlável, ou seja, que só possuísse a variável \(s\) no domínio de Laplace. Para projetos de engenharia "de verdade", os motores costumam ter seus parâmetros disponíveis em datasheets (folhas de dados). Nos pequenos projetos domésticos, boa sorte pra quem quer encontrar algo bem especificado. Quando/se encontrar, vai ser caro.

Assim, precisamos aplicar algumas teorias de identificação para modelar o motor matematicamente e aplicar alguns experimentos bem práticos para determinar o valor das constantes do motor.

Modelagem matemática do motor

Para controlar a velocidade de um motor DC é necessário obter sua função de transferência \(G(s)=\frac{\Omega(s)}{E(s)}\), onde \(\Omega(s)\) e \(E(s)\) são, respectivamente, as transformadas de Laplace (\(\mathcal L\)) da velocidade angular do eixo do motor \(\omega(t)\) e da tensão aplicada em seus terminais \(e(t)\).

Um modelo simplificado de motor (apresentado na figura 1) envolve uma resistência, derivada dos fios e dos contatos entre o rotor e as escovas, uma indutância devida aos enrolamentos dos fios e uma força contra-eletromotriz gerada pela rotação do eixo, de acordo com a lei de Lenz.

Na figura:

\(\omega(t)\) é a velocidade angular [rad/s]
\(E(s)\) é a tensão aplicada no motor [V]
\(R\) é a resistência interna do motor [\(\Omega\)]
\(K\) é a constante de torque do motor [V/(rad/s)]
\(J\) é a constante de inércia do conjunto do motor [Kg/m²].

Para motores comerciais de pequeno porte pode-se desprezar a indutância, pois a reatância indutiva \(\omega L\) é pequena em relação à resistência. Isso ocorre pois motores em geral não respondem a estímulos em frequências elevadas (acima de 40 Hz) e a indutância das bobinas é baixa (abaixo de 1 mH).

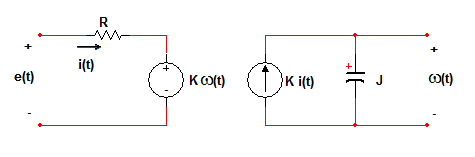
Figura 1: Parte elétrica (esquerda) e análogo elétrico da parte mecânica (direita).

Do lado esquerdo do circuito elétrico e pela Lei de Ohm temos que:

\begin{equation} i(t)=\frac{e(t)-K_m\omega(t)}{R} \label{eq_corrente} \end{equation}

Quando é utilizado um sistema de unidades coerente, como é o caso do SI, os valores das constantes de força contra-eletromotriz e de torque são iguais. Por isso, daqui para frente, elas são chamadas apenas de \(K\).

\begin{equation*} K_m=K_p=K \end{equation*}

O torque gerado é proporcional à corrente na armadura do motor, então:

\begin{equation*} T(t)=K i(t)=\frac{K e(t)-K^2\omega(t)}{R}=J\dot{\omega}(t) \end{equation*}

reagrupando os termos, obtemos:

\begin{equation*} RJ\dot{\omega}(t)+K^{2}\omega(t)=Ke(t) \end{equation*}

A transformada de Laplace da equação acima, considerando condições iniciais nulas, é dada por:

\begin{equation*} (RJs+K^2)\Omega(s)=KE(s) \end{equation*}

logo,

\begin{equation} \Omega(s)=\frac{K}{RJs+K^2}E(s)=\frac{\frac{K}{RJ}}{s+\frac{K^2}{RJ}}E(s) \label{eq_omega_laplace} \end{equation}

assim obtemos um modelo para o comportamento do motor. Deve-se agora determinar o valor das constantes, o que será feito através dos experimentos a seguir.

A determinação das constantes \(R\) e \(K\) é feita através de experimentos utilizando apenas medidas em regime estacionário, utilizando os dados para realizar uma regressão linear. Disto obtém-se retas cujas tangentes são os valores desejados.

Para obter \(R\), nota-se que, a partir da equação

\begin{equation*} R=\frac{e(t)-K\omega(t)}{i(t)} \end{equation*}

Para anular o termo da força contra-eletromotriz, podemos então travar o eixo do motor. Assim,

\begin{equation} R=\frac{e(t)}{i(t)} \label{eq_resistencia} \end{equation}

o que será usado no primeiro experimento.

Ao aplicar uma tensão fixa nos terminais do motor, o mesmo irá adquirir velocidade até esta se estabilizar em um valor. Isto pode ser utilizado para determinar o valor da constante de força contra-eletromotriz \(K\). Matematicamente, fazendo \(E(s)=Eo/s\) (fazendo o sinal de referência ser um degrau com amplitude \(E_0\), ou seja \(e(t)=E_0 u(t)\)) na equação \ref{eq_omega_laplace} e aplicando o Teorema do Valor Final, obtém-se, no regime estacionário,

\begin{equation*} \lim_{t\rightarrow\infty} \omega(t)=\lim_{s\rightarrow 0} s\Omega(s)= \lim_{s\rightarrow 0}s \frac{K}{RJs+K^2}\frac{E_0}{s}= \lim_{s\rightarrow 0}\frac{K}{RJs+K^2}E_0=\frac{KE_0}{K^2}=\frac{E_0}{K} \end{equation*}

logo, no regime estacionário (\(t\rightarrow\infty\)),

\begin{equation} K=\frac{E_0}{\omega} \label{eq_K} \end{equation}

Assim, podemos plotar um gráfico tensão \(\times\) velocidade, e de sua tangente obteremos o valor de \(K\). Isto será feito no experimento 2.

Já para obter o valor da constante \(J\), podemos verificar o comportamento temporal de \(\omega(t)\). Separando em frações parciais a equação \ref{eq_omega_laplace}, temos:

\begin{equation*} \Omega(s)= \frac{1}{s}\frac{\frac{K}{RJ}E_0}{s+\frac{K^2}{RJ}}=\frac{A_1}{s}+\frac{A_2}{s+\frac{K^2}{RJ}} \end{equation*}

\begin{equation*} A_1=\frac{\frac{K}{RJ}E_0}{\frac{K^2}{RJ}}=\frac{E_0}{K} \end{equation*}

\begin{equation*} A_2=\frac{\frac{K}{RJ}E_0}{-\frac{K^2}{RJ}}=-\frac{E_0}{K} \end{equation*}

Logo,

\begin{equation*} \Omega(s)=\frac{\frac{E_0}{K}}{s}+\frac{-\frac{E_0}{K}}{s+\frac{K^2}{RJ}} \end{equation*}

Realizando a transformada inversa de Laplace

\begin{equation} \omega(t)=\frac{E_0}{K}\left(1-e^{-\frac{K^2}{RJ}t}\right) \label{eq_omega_tempo} \end{equation}

Como já temos os valores de \(R\) e \(K\), podemos realizar um experimento para determinar \(J\), observando a resposta do motor no transiente de uma entrada degrau. Isto é o experimento 3.

Observação 1: a constante de tempo da equação exponencial será \(\tau=\frac{RJ}{K^2}\).

Observação 2: a equação \ref{eq_omega_tempo} é um valor constante menos uma curva exponencial. Isto pode ser utilizado para preparar os dados obtidos no experimento, para fazer um curve fit linear ou exponencial.

Preparação

Como todo procedimento experimental, há alguns detalhes que devem ser preparados com antecedência, para evitar perder tempo durante a execução do experimento.

Primeiramente, deve-se ter:

Motor a ser testado
Sensor de velocidade angular para o motor
Fonte de tensão DC ajustável
Amperímetro e voltímetro
Computador (recomendável ter o MATLAB instalado)

O sensor de velocidade angular para o motor pode ser em várias formas. Pode-se ter um sensor de velocidade acoplado através de engrenagens, ou outro motor de características conhecidas acoplado por polias, ou, como foi utilizado neste experimento, um encoder de quadratura.

Um encoder de quadratura, mais especificamente um conjunto com dois sensores de efeito Hall, mede a variação da posição angular do motor, gerando em sua saída duas ondas quadradas.

Quando estas duas ondas são combinadas, elas podem ser interpretadas como um valor em código Gray de dois bits. Interpretando este código como um código cíclico, pode-se inferir que quando o valor se desloca para um lado o motor se moveu em um sentido e vice-versa, como mostrado na figura 2.

Figura 2: Saída do encoder interpretada como um código Gray.

Outra forma mais simples (e normalmente com menos ruído) de se ler a saída de um encoder de quadratura é observar seu comportamento nas bordas da onda, mais precisamente em apenas uma das bordas de uma das ondas. Por exemplo, pode-se observar a borda de subida da onda na primeira saída do encoder. Quando houver esta borda de subida, verifica-se a situação da onda na segunda saída do encoder. Se a segunda saída estiver em nível alto, o motor girou um passo do encoder em uma direção. Se a segunda saída estiver em nível baixo, o motor girou na outra direção (figura 3). O tempo entre uma borda de subida e a próxima determina a velocidade em termos de passos, da qual se obtém a velocidade angular ao se dividir pelo número de passos para se completar uma volta.

Figura 3: Saída do encoder interpretada a partir de uma das bordas de subida.

Uma forma simples de se ler estas duas saídas é utilizar um microcontrolador. A placa utilizada para este fim foi o Arduino Uno, que é uma plataforma bastante popular e de fácil programação.

O programa utilizado está em anexo, com comentários. Seu funcionamento é baseado em uma interrupção de mudança de pino, onde é implementado o método por bordas da figura 3.

A leitura da velocidade da roda se dá basicamente em dois modos. O modo de operação pode ser mudado facilmente trocando-se apenas um parâmetro de configuração.

O primeiro modo, que foi chamado de STEP_TIME realiza a contagem de pulsos a cada segundo, obtendo a velocidade em radianos por segundo a partir da fórmula

\begin{equation*} \omega=\frac{2\pi\times\textrm{passos em um segundo}}{\textrm{passos por volta}} \textrm{[rad/s]} \end{equation*}

Este modo é utilizado para se obter maior precisão da velocidade no regime estacionário, em que a velocidade não se altera durante a medição. Por isso, é utilizado no experimento 2.

Já o segundo modo, chamado de TIME_STEP, mede o tempo gasto entre cada passo, obtendo então a velocidade a partir da fórmula

\begin{equation*} \omega=\frac{2\pi 10^6}{\textrm{passos por volta}\times\textrm{tempo do passo em microssegundos}} \textrm{[rad/s]} \end{equation*}

Este modo é utilizado quando há necessidade de leituras mais rápidas, como é o caso do transiente medido no experimento 3. No entanto, é menos preciso pois há variacões maiores devido às imperfeições do encoder.

Para se obter o número de passos por volta do encoder utilizado, foi medido o número de passos enquanto se girou a roda por 100 voltas. O número de passos ao final foi dividido pelo número de voltas realizadas, neste caso obtendo-se o valor de 390 passos por volta.

Por fim, os dados medidos são dispostos em colunas separadas por tabulação e enviados através da porta serial. Neste formato, fica fácil copiá-los e colá-los em uma planilha ou mesmo direto no MATLAB.

Procedimentos na prática

Temos a função de transferência simplificada para um motor DC qualquer, da equação .

\begin{equation} G(s)=\frac{\Omega(s)}{E(s)}=\frac{K}{R J s+K^2}=\frac{\frac{K}{RJ}}{s+\frac{K^2}{RJ}} \label{eq_funcao_transferencia} \end{equation}

Para obter as características de um motor específico, ou seja, para obter as constantes da equação do motor, devemos fazer alguns experimentos.

Experimento 1

O primeiro experimento determinará a resistência interna do motor. Em princípio, colocar um multímetro na função de ohmímetro nos terminais do motor seria suficiente, mas na realidade, esta medida pode fornecer dados incorretos (neste experimento a diferença em um dos motores foi de 833%).

Dados melhores podem ser obtidos da seguinte forma:

Ligar os terminais do motor em uma fonte de tensão ajustável, colocando um amperímetro em série com o motor para medir a corrente.
Aumentar a tensão até que o motor comece a rodar.
Segurar o motor de forma que ele fique parado. Cuidado para não se ferir nesta operação caso o motor seja muito forte.
Verificar a corrente que passa pelo motor através do amperímetro. O valor deve ser anotado apenas quando ele se estabilizar.
Executar os três passos anteriores para outras tensões intermediárias. A tensão não deve ultrapassar a especificação do motor. Também não é recomendado chegar muito próximo à máxima tensão no motor, pois assim a corrente que passará na bobina será muito elevada, e esta pode ser danificada devido ao calor excessivo causado pelo efeito Joule.

Com os dados de corrente \(\times\) tensão, é possível obter um gráfico próximo a uma reta (figura 4). De acordo com a equação \ref{eq_resistencia}, verifica-se que da inclinação do gráfico pode-se obter a resistência do motor.

Figura 4: Gráfico do experimento 1.

Por exemplo, a partir de duas medidas,

\begin{equation*} R=\frac{\Delta e}{\Delta i}=\frac{e_2-e_1}{i_2-i_1} \end{equation*}

Para o motor avaliado no experimento, a partir de uma única medida, obteríamos

\begin{equation*} R=\frac{6-0}{1.09-0}=5.505 [\Omega] \end{equation*}

Utilizar mais pontos em geral nos dará maior precisão e para obter a inclinação da reta, pode-se utilizar uma ferramenta de regressão linear. O Microsoft Excel possui recursos deste tipo. Também há uma ferramenta no MATLAB chamada Curve Fitting Tool que pode ser usada para isto. O comando para abrí-la é cftool. Outra forma mais rápida para regressão linear direto pela linha de comando do MATLAB é usando o comando polyfit, neste caso para uma regressão linear, usaremos o parâmetro N=1:

>> V1=[4 5 6];
>> I1=[0.62 0.88 1.09];
>> polyfit(I1,V1,1)

ans =

    4.2393    1.3400

A saída significa que uma regressão linear, da forma \(Ax+B\), para os pontos utilizados, equivale a uma reta onde \(A=4.2393\) e \(B=1.34\).

Como a inclinação da reta é o valor de \(R\), temos que \(R=4.2393[\Omega]\). Note também que na reta obtida (figura 5) há um deslocamento da reta, causada principalmente pelos atritos do sistema (estático e viscoso).

Figura 5: Gráfico do experimento 1, incluindo as retas com o R obtido.

Experimento 2

O segundo experimento nos dará a constante \(K\). Este experimento consiste basicamente do mesmo procedimento que o primeiro, porém sem segurar a roda, deixando-a correr livremente. Ainda, em vez de medir a corrente no motor, será medida a velocidade da roda, em radianos por segundo. Assim, no regime estacionário, podemos nos utilizar da equação \ref{eq_K} e de um gráfico tensão \(\times\) velocidade.

Para isto foi utilizado o Arduino, lendo a velocidade a partir do encoder, no modo STEP_TIME.

A partir dos dados obtidos no experimento, é possível obter a constante \(K\) através de regressão linear, da mesma forma que foi feito para o experimento anterior. Obtem-se então o gráfico da figura 6 através do comando

K=polyfit(Vel2,V2,1)

Figura 6: Gráfico do experimento 2, com os pontos lidos no experimento e a reta obtida.

Com isto é obtido o valor \(K=0.5419\) [V/(rad/s)], como o motor não está com carga, a tensão pode ser aumentada até o máximo da especificação do motor. Este valor máximo deve ser obtido também para uso no terceiro experimento.

Uma outra forma, mais simples porém menos precisa, é simplesmente aplicar uma tensão no motor, esperar o regime estacionário (velocidade constante), medir a corrente no sistema, descontar a queda de tensão na resistência causada por esta corrente e aplicar a fórmula \(K=E_0/\omega\) da equação \ref{eq_K}. No entanto, devido à importancia da constante \(K\) e às não-idealidades do motor (como a tensão mínima antes do motor começar a rodar), é melhor utilizar o método anterior. Essas não-idealidades também podem ser visualizadas na figura 6 como um deslocamento da reta.

Experimento 3

O terceiro experimento será usado para obter a constante de inércia \(J\).

Conforme visto na seção de modelagem matemática, ao aplicar um degrau de tensão, o motor responderá em velocidade com uma curva exponencial invertida, da forma da equação \ref{eq_omega_tempo}.

Com todas as demais constantes determinadas, obtendo-se a curva para esta função também é possível obter matematicamente a constante que falta, \(J\).

Assim, este experimento será exatamente como a teoria sugere:

Aplicar um degrau de tensão nos terminais do motor, com o valor máximo especificado (o que nos dará a velocidade máxima sem carga).
Medir a velocidade da roda no transiente, ou seja, enquanto ela acelera até chegar ao regime estacionário. Esta medição pode ser feita com o Arduino lendo o encoder no modo TIME_STEP.
Com as medições e o tempo de cada medição, é possível realizar uma regressão exponencial, ou tratar os dados para fazer outra regressão linear.

O tratamento inicial dos dados é feito para se obter uma exponencial pura. Nossos dados estão na forma da equação \ref{eq_omega_tempo}. Para obtermos nossa exponencial pura, devemos ter o valor de \(\omega_0\), obtido com um degrau de mesmo tamanho no experimento 2 (ou no regime estacionário deste experimento, porém os dados do experimento 2 são mais precisos por usar o modo STEP_TIME). Assim,

\begin{equation*} \omega(t)=\frac{E_0}{K}\left(1-e^{-\frac{K^2}{RJ}t}\right) \end{equation*}

\begin{equation*} f(t)= 1 - \frac{\omega(t)}{\frac{E_0}{K}} = e^{-\frac{K^2}{RJ}t} \end{equation*}

A regressão exponencial também pode ser feita através da ferramenta Curve Fitting Tool do MATLAB (chamada usando o comando cftool). Alternativamente, pode-se usar diretamente a função de regressão exponencial com o comando fit com 'exp1' como terceiro parâmetro.

Os comandos para obter diretamente os valores são:

E0 = V2(end);
f = -Vel3/(E0/K(1))+1;
K2RJ = fit(T3,f,'exp1');
J = -K(1)^2/(Rb(1)*K2RJ.b);

Assim obtemos o valor de \(J=0.0047\) [N m²]. Substituindo todos os valores na equação original (\ref{eq_omega_tempo}), traçamos o gráfico da figura 7.

Figura 7: Gráfico do experimento 3, com os pontos lidos no experimento e a curva exponencial.

Para esta regressão, o Excel também pode ser utilizado, porém seus resultados são piores, uma vez que o Excel só permite utilizar dados positivos, enquanto uma boa regressão também terá como entrada valores negativos após a preparação dos dados. Caso o MATLAB não esteja disponível, pode-se melhorar o resultado do Excel tratando-se os dados mais uma vez e fazendo uma regressão linear em vez de uma regressão exponencial, da forma:

\begin{equation*} f_L(t) = \ln(f(t)) = -\frac{K^2}{RJ}t \end{equation*}

e assim obter \(K^2/RJ\) a partir da inclinação da reta, calculando, por fim, \(J\).

Para finalizar, podemos substituir os valores obtidos para as constantes \(R\), \(K\) e \(J\) na função de transferência da equação \ref{eq_funcao_transferencia}.

\begin{equation*} G(s)=\frac{\Omega(s)}{E(s)}=\frac{\frac{K}{RJ}}{s+\frac{K^2}{RJ}}= \frac{\frac{0.5419}{4.2393 \cdot 0.0046}}{s+\frac{0.5419^2}{4.2393 \cdot 0.0046}} =\frac{27.20}{s+14.74} \end{equation*}

Observação:

Note que os números do numerador e do denomidador diferem exatamente do fator \(K\) encontrado anteriormente. Isto pode ser visto mais claramente na equação \ref{eq_funcao_transferencia}}. Como mostrado na equação \ref{eq_K}}, \(K\) corresponde exatamente à proporção entre o sinal de tensão aplicado no motor e sua velocidade no regime estacionário. É importante ter isto em mente ao projetar um controlador, pois, de forma geral, quando se mede a resposta ao degrau unitário, o erro será calculado esperando-se na saída um valor também de amplitude unitária, o que não acontece neste sistema. Para resolver isto, deve-se multiplicar o valor medido pelo sensor por \(K\), ou multiplicar o valor de referência por \(1/K\).

Este documento está disponível online em sua última versão em:

http://ronan.dapaixao.com.br/artigos/2011/08/19/identificacao-de-motores/.

Anexos

Programa do Arduino